Players of the fantasy trading card game Magic: The Gathering can arrange their deck of cards before they are shuffled to seek an unfair advantage. But should such pre-round “manaweaving” be considered cheating?
Magic: The Gathering (M:TG) is a fantasy trading card game (TCG) developed in the early 90’s by Dr. Richard Garfield1 and distributed by Wizards of the Coast. It is considered the most successful game of its genre, boasting more than 40 million players worldwide and $1 billion in 2023 revenue. The general gameplay of M:TG begins with two opposing players shuffling their respective customised decks of 60 cards. Afterwards, they each offer their shuffled deck to their opponent for the latter to cut and/or shuffle. Each player then draws 7 cards from their deck as their opening hand and the game proceeds.
The game has a vibrant competitive scene, with tournaments held regularly in local games stores across the world that build up to regional championships and, ultimately, professional tours with prize purses worth up to $500,000. With such significant prizes on the line, competitive M:TG play adheres to a strict set of rules called the Magic: The Gathering Tournament Rules (MTR). In this article, I explore the aspect of the MTR that deals with deck shuffling, particularly as it pertains to initial randomisation of a player’s deck. I discuss a practice called “manaweaving,” whereby a player initially arranges the order of their deck prior to the start of a match. I examine the extent to which this practice provides some unfair advantage and should be considered cheating.
What is manaweaving and is it allowed?
The typical M:TG deck is composed of two types of cards: land and non-land cards. Land cards or simply “lands” are resources that are needed to be able to use the non-land cards, also referred to as “spells.” Thus, ideal opening hands are composed of 2-3 lands and 4-5 spells. Manaweaving is the practice of arranging the deck so that it is composed of some interchanging sequence of lands and spells.
According to the MTR, the initial ordering of a deck does not matter, as a player is required to randomise their own deck by shuffling. The MTR also states that after a player randomises their deck, the opponent may shuffle the deck as well, or ask a tournament judge to do so. Thus, the MTR currently does not care about the initial order of a deck, and so a player may manaweave prior to the start of a tournament round without penalty. They are required to shuffle sufficiently to randomise the deck and, indeed, if a deck is randomised successfully, then by definition the initial order of the deck would not have any impact on the final order of the deck. Regarding how to shuffle the deck, the MTR does not explicitly provide any procedure. Fortunately, literature on proper shuffling is quite extensive, with seminal work2 recommending the minimum number of riffle shuffles to randomise a deck to be [math]\frac{3}{2}log_2 N[/math], where N is the number of cards in a deck and a riffle shuffle is a shuffle whereby the deck is divided into two piles at random and then the two piles are combined together in some alternating fashion. With 60 cards, [math]\frac{3}{2}log_2 N[/math] = 8.86 or at least 9 shuffles.
Effect of riffle shuffles after manaweaving
Without any shuffling, manaweaving for a 60-card deck with 20 lands and 40 spells will always provide a player with a hand that consists of 2 lands and 5 spells. There are three simple configurations to a manaweaved deck. These are repeated sequences of spell-spell-land, land-spell-spell, or spell-land-spell. If a “perfect” riffle shuffle is performed, whereby the deck is cut exactly in half and the two halves are perfectly combined in alternating fashion together, then the number of lands in the opening hand will be a deterministic sequence depending on the initial configuration. A snapshot of this sequence for each configuration is provided in Table 1. This sequence repeats after 58 shuffles.

Suppose the player and then the player’s opponent subsequently perfectly riffle shuffles the player’s initially manaweaved deck. The number of lands in the player’s opening hand would then be a random variable X determined by the initial configuration and the number of riffle shuffles performed. We can thus measure whether the manaweaving has an effect by computing the probability that X=2 or X=3; the typical ideal scenario for the opening hand. Assuming that each number of perfect riffle shuffles is equally likely, the probability can be computed directly by taking the proportion of outcomes among the first 58 that are either 2 or 3. This was done for the three typical manaweaved starting configurations and shown in Table 2. Also shown in Table 2 is the probability if the starting configuration of the deck was completely randomised, which is computed from a hypergeometric distribution with corresponding parameters.
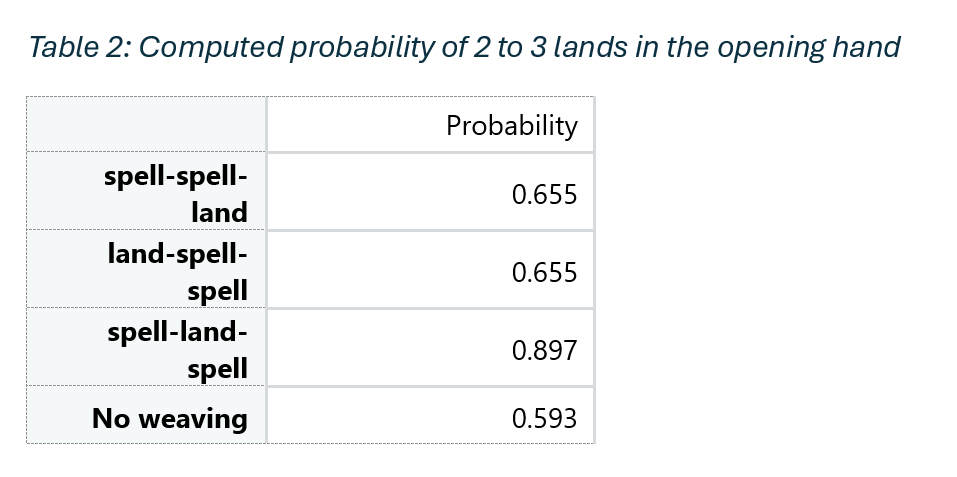
Table 2 shows that, without any weaving, the probability of getting 2-3 lands in the opening hand is 0.593. In contrast, each of the manaweaved decks has a higher chance of getting a hand with 2-3 lands, with the probability of doing so when using the third configuration as high as 0.897!
Of course, these results assume that both players are doing perfect riffle shuffles. While not impossible to do, performing a perfect riffle shuffle takes practice, and only the player who owns the deck has an incentive to do perfect riffle shuffles on their deck to benefit from manaweaving. To explore the effect of more realistic shuffles, we can use the Gilbert–Shannon–Reeds (GSR) model, which incorporates randomness both in how the deck is cut into two piles and how the cards in those two piles are interwoven3. I simulated using the GSR model to estimate the same probability of getting 2 or 3 lands in the opening hand.
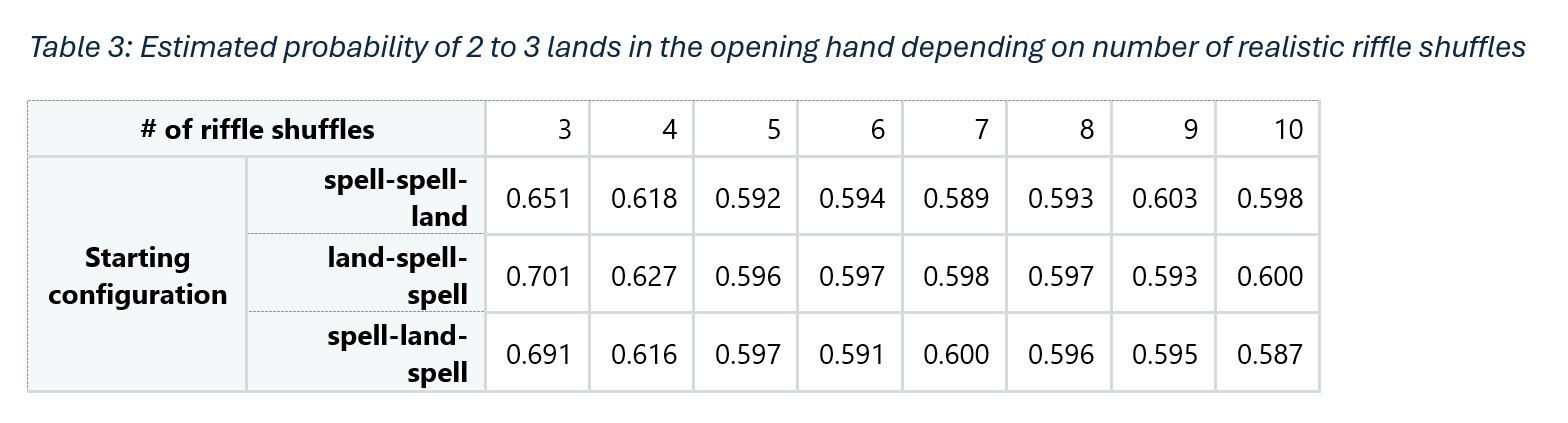
Table 3 shows that three GSR shuffles are insufficient to remove the advantage from manaweaving regardless of initial manaweaving configuration, but that the advantage is diminished as more GSR shuffles are performed, and that the probability of getting 2 to 3 lands does not differ considerably from what is expected of a fairly-shuffled deck after the recommended 9 shuffles.
Conclusion? Be sure to shuffle
Through directly calculating relevant probabilities or estimating them from simulation, I have shown that manaweaving creates an unfair advantage that is retained when performing perfect riffle shuffles even if the number of shuffles is random. Rules from the MTR dictate that a player is responsible for making sure that their deck is properly randomised before presenting it to their opponent for a cut or shuffle, but someone trained to do perfect shuffles can convincingly provide the appearance of shuffling thoroughly without losing the advantage set up by their deck’s starting order. This underscores the need for M:TG players, especially in high-stakes tournaments, to sufficiently shuffle their opponent’s deck when presented. Regardless of any sort of rigging that their opponent may have been able to perform, riffle shuffling “imperfectly” at least 9 times for 60-card formats is enough to bring a deck to a random state on average.
While results in this article show that the advantage is diminished by proper shuffling, there is no logical reason to perform a manaweave except to hope that one is both capable of riffle shuffling well enough to retain the manaweaving advantage and the opponent does not shuffle well enough to diminish the advantage. This hope represents intent to end up starting with an insufficiently randomised deck, and such intent already violates the current MTR but is not practically enforceable. Ultimately, there is no good reason to perform manaweaving, and a stronger stance against it can be built by creating greater awareness on the importance of sufficiently shuffling an opponent’s deck when it is presented.
References
- Zilio, F., Prates, M., Lamb, L. (2018). Neural Networks Models for Analyzing Magic: The Gathering Cards. In: Cheng, L., Leung, A., Ozawa, S. (eds) Neural Information Processing. ICONIP 2018. Lecture Notes in Computer Science(), vol 11302. Springer, Cham. doi.org/10.1007/978-3-030-04179-3_20
- Bayer, D., Diaconis, P. Trailing the Dovetail Shuffle to its Lair. Ann. Appl. Probab. 2 (2) 294 – 313, May, 1992. doi.org/10.1214/aoap/1177005705
- Diaconis, P. Group Representations in Probability and Statistics. Lect Notes-Monogr Ser. 1988;11:i-192.
Mark Louie F. Ramos is assistant professor in the Health Policy and Administration Department at Pennsylvania State University, USA.
You might also like: Boxing with George Box




