
1. We wanted to have some direct evidence on World Cup games; we restricted it to the last six WCs which all have a very similar format (with a first round of games and then a knockout stage, starting with a round of 16).
2. We also want to have evidence on most recent performances of the teams affiliated with FIFA.
I think it's worth noting that many people (eg Goldman Sachs or FiveThirtyEight) who have had a go at a similar exercise have decided to discard friendlies. But it seems to me that these may be indicative of some general trend and so we decided to keep them in our dataset.
The main outcome of our model is the number of goals scored by each team in each of the games. In particular, we want to account for the fact that the two counts are correlated. We model
where is the number of goals scored in game . Note that we replicate the same game twice, looking at it from each of the two teams' perspective, respectively. So, for example, the first game in the dataset is Argentina vs Cameroon, the opening game of Italia 90 and the first two rows in our dataset describe the game from the perspective of Argentina and Cameroon, respectively, like so:
| Game | Team | Opponent | Goal | … |
| 1 | Argentina | Cameroon | 0 | … |
| 1 | Cameroon | Argentina | 1 | … |
The 'propensity' of the team in row to score when they play against the team in row , which we indicate as , is modelled as
The linear predictor is made by:
1. The overall intercept ;
2. A set of unstructured effects β, accounting for the effect of i) playing at home, away or on neutral ground (Home and Away are dummies, so that when they are both 0, then the game is played on neutral ground); ii) the type of the game, which could be 'finals' (World Cup or Continental tournament, or the Confederation Cup), or 'other' (including friendlies and qualifiers); iii) the difference in recent forms between the two opponents − this is computed by accounting the mean number of points obtained in the last two games played by each team. These are rescaled in the interval [0;1] so that the difference is a continuous variable defined in [-1;1] (a value of 1 indicates that a team is much more 'in form' − and thus potentially stronger − than their opponent for that game);
3. A set of structured effects and these are team-specific random effects, modelled as exchangeable. Effectively, they can be interpreted as 'attack' (for the team) and 'defence' (for the opponent) strength.
We fit a Bayesian model (using INLA to speed the computation up − it runs quite smoothly and quickly; about 30 seconds on a medium range computer).
Then, for each of the future games (ie those to be played starting this week) we can simulate from the posterior distributions of the linear predictors . When opportunely rescaled, these can be used to simulate the number of goals scored in the next games by the two teams playing.
In particular, given evidence that at the World Cups usually fewer goals are scored, we have inflated the chance of seeing a 0, so that the prediction is made as
Where is given an informative distribution based on the assumption that the chance of excess 0s in the observed number of goals at the World Cup is centered around 0.035 with a standard deviation of 0.02 − in actual facts, we've tried a few alternatives, but this assumption does not affect the estimation/prediction massively.
In addition, for the yet-to-be-played games, the value of the 'recent form' variable (which sort of determines the difference in strength between the two teams playing in a game − we indicate this as and for teams and , respectively) is based on an evidence synthesis of the available odds for each of the team, rather than on the actual past 2 games. It is easy to find data on lots of bookies offering odds for each of the 32 teams involved in the WC − we've based our evidence synthesis on the 20 values.
I think there is a good reason for doing this: the last two games observed in the dataset are friendly games played in preparation for the finals. In those games, teams tend to train really, but do not give their 100%. On the other hand, the valuations of the bookmakers should be a more reliable indication of the actual relative strength of the teams involved at the moment.
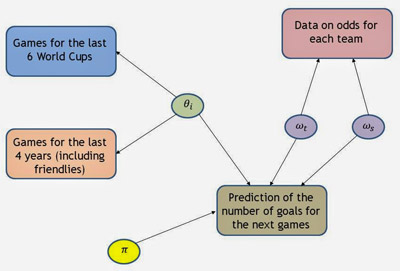 Thus, we decided to use those values (starting from the odds, we built a simple log-Normal model and then rescaled the team-specific effects in the scale [0;1] to indicate the 'recent form' of the teams). Under this sub-model, Brazil has a score of recent form of 0.97, closely followed by Argentina with a score of 0.96. The weakest team are Costa Rica, with a score of 0.044. If you're into graphical representations for models, here's one for you on the right.
Thus, we decided to use those values (starting from the odds, we built a simple log-Normal model and then rescaled the team-specific effects in the scale [0;1] to indicate the 'recent form' of the teams). Under this sub-model, Brazil has a score of recent form of 0.97, closely followed by Argentina with a score of 0.96. The weakest team are Costa Rica, with a score of 0.044. If you're into graphical representations for models, here's one for you on the right.
Rather than predicting all the way to the final based on the model and data available right now, we decided to take it step by step. I think there is a very good argument to do so. In fact, it is quite likely that recent form will be modified by the games that will be played in the course of the first round.
For example, Group D (including Uruguay, Costa Rica and my personal derby of England and Italy) is arguably the closest with 3 relatively strong teams (FiveThirtyEight seem to think so too). So, if Italy beat England on Saturday this surely will swing the odds in their favour, thus probably modifying quite massively the behaviour of the other teams in the next games (eg if England lost on Saturday, then they'll have to win their next game against Uruguay, while Italy may be happy to get a draw against Uruguay in their final game of the round, etc…).
So, in order to make more sense of the model, we'll only predict batches of games; before any game is played and based on the current model and data, we'll predict the first 16 games to be played − that's when all the finalists will have played their first game. Then we will update the recent form variable based on the observed results and re-run the model to predict the next batch of 16 games. And then we'll repeat this step again and predict the final batch of 16 games for the group stage.
This article first appeared on Gianluca Baio’s personal blog.




