
With 37 balls remaining and three wickets in hand, England had 54 more runs to make. A run rate of nine an over, while challenging, was not outside the range of what the teams had been scoring in the final overs of innings in the series, albeit with fewer wickets lost. The team’s two batsmen were in form scoring at more than the required rate.
Then rain intervened and ate up 20 minutes of the remaining match time, which meant that the umpires had to make a calculation to allow the match to resume and play out to a result. Applying the Duckworth-Lewis adjustment method, the target was reduced from 54 runs required to 34 but the number of deliveries left was reduced to 13. From having to score roughly nine an over across six overs the team was now being asked to score roughly 16 an over for two. To many the adjustment seemed unfair. Despite having been in with an arguable chance before the interruption, the task now seemed to be at the boundaries of feasibility.
England lost a very close game – and Eoin Morgan, England’s one-day captain, bemoaned the way the rule had worked:
‘Do I understand Duckworth-Lewis? No. Absolutely. I don’t think anybody does … It’s a part of the game that you can’t change. It’s a calculation that’s always there … As the game evolves as much as it has done, particularly in 50-over cricket, Duckworth-Lewis could certainly be looked at.’
He is not the first captain to express puzzlement – Indian captain, M S Dhoni is also on record as saying: ‘Frankly speaking, I don’t understand Duckworth-Lewis.’
Putting aside the question of fairness, it is surely a problem that the outcomes of a major international sport are determined by a rule that captains struggle to understand.
Method – or madness?
The Duckworth-Lewis method, a scheme devised by statisticians Frank Duckworth and Tony Lewis (and lately modified by Steve Stern), was invented in the 1990s as a replacement for alternative rules on what to do if it rained with lamentable histories of ridiculous consequences.
It was without any doubt a massive improvement – meaning that limited overs cricket games interrupted by rain could proceed reasonably sensibly even if all the overs couldn’t be bowled. However regrettable Friday’s outcome might have been, it bears no comparison with the absurdities perpetrated under previous rules – such as when South Africa’s task of 22 from 13 balls was reduced after brief rain to 21 required off a single delivery in a notorious World Cup semi-final against England in 1992. In my view, it also remains superior to other often-mooted replacements.
Duckworth-Lewis is based on the idea of compensating rain-affected teams for the loss of ‘run-scoring resources’. This is interpreted by reference to the runs that would have been scored by an average team facing the lost deliveries. Specifically, whichever innings the interruption occurs in, the reference point is the scoring rate of a team with similar wickets in hand setting a target in the first innings. Applied as in this game to a second innings interruption, the rule adjusts the target down so as to take away the fraction of a typical first innings score that would have been achieved in overs comparable to those lost.
What the method does not do is keep constant the likelihood of each team winning. That is intentional – Duckworth and Lewis explicitly disavow the idea.
As games proceed, it is common to see the Duckworth-Lewis ‘par score’ reported and interpreted as the score needed for a team to be somehow ahead in the game. This is a dubious interpretation. What the par score tells you is who would win if the game were stopped now and decided under Duckworth-Lewis. What it doesn’t tell you is who would be most likely to win if the game continued uninterrupted.
If it strikes you as odd that those are not the same thing, then you understand the rationale behind an alternative idea – that of a rule which preserves probabilities of victory.
Winning formula
A rule that adjusts scores to keep likelihoods of winning unchanged has been proposed in the past by myself and co-author, Jonathan Thomas, as well as by others. The idea is not wholly dissimilar in spirit to that of Duckworth-Lewis.
It acknowledges that loss of run-scoring resources needs to be compensated, but resources are valued in terms of what matters to teams, which is the probability of winning, rather than – as under Duckworth-Lewis – the expected run total in one of the innings. Unlike Duckworth-Lewis, whose rule is not strategically neutral, such a rule also has the advantage of making no difference to the optimal strategy of a team aiming to win the match.
Such a rule would necessarily adjust targets differently depending on how many runs have already been scored. Duckworth-Lewis adjustments do not do that. It is indeed consequently possible under Duckworth-Lewis for teams to come back after an interruption with one team having already won – England would have done so had they already scored, before the rain on Friday, the 34 more runs required after application of Duckworth-Lewis. This fact alone makes transparently clear that probabilities of victory are not preserved.
Duckworth and Lewis colourfully criticise the idea that adjustments might recognise runs already scored as ‘socialist’: ‘taxing the run-rich to aid the run-poor’ by rewarding underperforming teams with bigger target reductions. But this argument simply presupposes that runs rather than probabilities are the appropriate currency in which to be thinking.
Level playing field
In my work with Thomas, we estimated a model of how winning probabilities evolve under optimum batting and used it to calibrate a probability-preserving rain rule. The data we used came from domestic English 40-over cricket in 1996. Things have changed enormously since, especially since the introduction of Twenty20 cricket – so the rule would surely need recalibration.
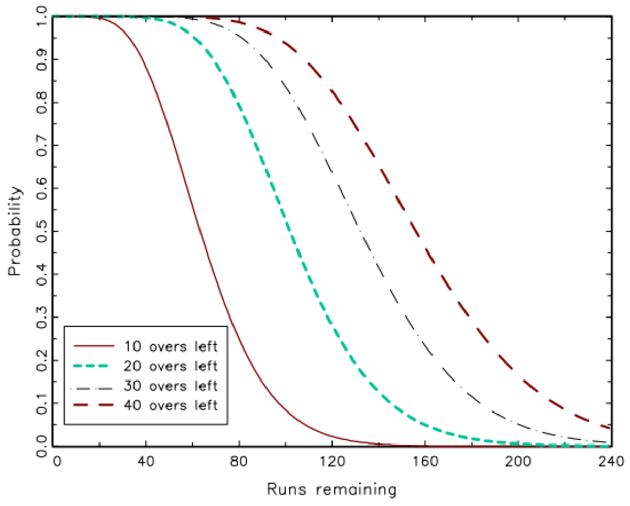
How probability works: the likelihood of winning a second-inning chase with three wickets lost (for an English county team in 1996
Nonetheless, we show that the rule we proposed suggests adjustments that are usually not very different to Duckworth-Lewis and that this is not surprising since there is close to mathematical equivalence in typical circumstances if interruptions are small enough. The difference only shows up for significant interruptions like that on Friday.
Scoring nine an over during the final six overs with only three wickets in hand was close to unprecedented in 1996, and the probability of achieving it was therefore assessed as remote. We can still ask how many would have needed to have been scored off the final two overs for the probability to have been comparably small.
The answer is about 26 runs. So England would have been asked to score at 12 runs per over rather than 16 as it turned out. Not too much should be read into this since only re-estimation with more recent data could do justice to changing tactics and skills but it does seem that a more sensible target might have been set.
So, all questions of who should have won the game aside, Morgan is right when he suggests it is time to reassess the fairness of the Duckworth-Lewis rule and maybe replace it with something players, officials and spectators can better understand.
![]()
This article first appeared on The Conversation website.




