
The draw itself is very simple: teams are unseeded and are paired off against each other, with the first drawn team in each pair given the supposed advantage of playing the match on their home ground.
The BBC website recently published a feature using the FA Cup draw to highlight basic calculations in probability. As an example, in a round with 32 teams, the probability of any two teams being drawn to play each other is 1/31. The probability of a team being given a home draw four times in a row is (1/2)4, or 1/16.
While this calculation is correct, it does not immediately tell us about the probability of being given a home draw four times in a row in the same season, which is the more interesting question. Luton Town were once drawn at home 11 times in a row, but this would count for little had these matches all ended in defeat, and been spread across 11 different seasons.
As an alternative to the BBC’s calculation, we considered an alternative question: what is the probability that a team was drawn at home four times in a row, in the same season, given that they won in each of these four rounds?
This is a ‘conditional’ probability, and the distinction between the questions is important. As we expect a benefit from home advantage, we might expect the teams that reach the later stages of the competition to be the ones that have been lucky enough to be drawn at home.
Due to the format of the FA Cup, the leading clubs in England enter in the third round and must win four matches to reach the semi-finals. So they have four rounds where they must play matches either at home or away (the semi-finals and the final are always played on neutral grounds.)
To answer our question, we extracted data from all FA Cup competitions since 1925-26, the season when the current format was adopted.a For each of the four semi-finalists, we counted how many times in the previous four rounds (third round to sixth round) they had been drawn at home.
| Number of home and away draws of teams reaching the FA Cup semi-finals, seasons 1925-26 to 2013-14, and the number expected if there were no home advantage. | |||||
| 4 home |
3 home, 1 away |
2 home, 2 away |
1 home, 3 away |
4 away | |
| Number observed | 29 (9%) | 93 (28%) | 119 (36%) | 67 (20%) | 20 (6%) |
|
Number expected if no home advantage |
20.5 (6%) | 82 (25%) | 123 (38%) | 82 (25%) | 20.5 (6%) |
As the draw is random, if there were no effect of home advantage, we would expect to see the relative frequencies of 4, 3, 2, 1 and 0 home draws (out of 4) to follow a binomial distribution with probability equal to 0.5. The number of home draws would occur in the ratio 1:4:6:4:1. The number of instances that would be expected under this assumption appear in the final row of the table.
There are more instances of 4 or 3 home draws (out of 4) than would be expected given a probability of 0.5. So there is evidence of home advantage. In fact, the data are consistent with a probability of 0.53 of reaching the next round, given no other information about the strengths of the team involved. Therefore, although the effect of home advantage appears small, it is detectable given data across many seasons.
Now we can answer our original question. The probability of getting four home draws out of four, given that a team has reached the semi-finals, is 0.534 = 0.08, around 1 in 12. So we can expect to see it occur about once every three seasons.b
We also looked at whether the effect of home advantage changed over time. Although no consistent trend emerges, there is some indication of a greater effect of home advantage since 2000.
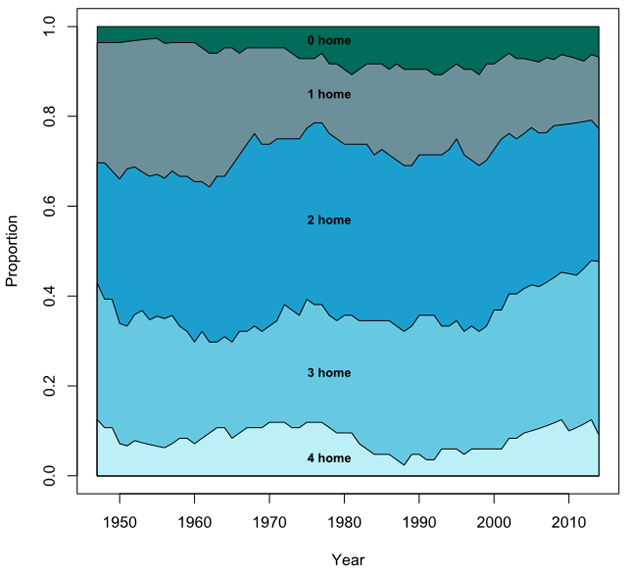
Proportion of home draws of teams reaching the semi-finals, seasons 1946-47 to 2013-14 (plotted as a moving average to reduce the visual effect of season-to-season variability).
If we restrict attention to the teams that won the competition each year, the same probability model fits equally well. During this period, only two clubs have won the FA Cup after they were drawn away from home in every round – Arsenal in 1971 and Manchester United in 1990.
Football supporters have a habit of looking for good omens at every turn, whether supported by evidence or not. So they should take note of Aston Villa's fortune this season, they are the only team in this weekend’s quarter-finals lucky enough to have been drawn at home in every round so far.
Footnotes
- a. We excluded the 1945-46 season when, uniquely, the format used two-legged home and away ties.
- b. Some caveats are required here. We have assumed that results in consecutive rounds are independent. We have also not considered the effect of teams being of different strengths. Indeed, we expect that to a large extent this explains why the effect of home advantage in the FA Cup appears to be weaker than in League competitions – strong teams are likely to beat weak teams whether they are playing at home or away.




