
In a recent article1, Anouk Claes and Marc de Ceuster reported the achievements of Nobel Prize Laureates in economics, which they estimated from their fame. They used a method which was originally published in Significance2. The method stems from the observation that the fame of fighter-pilot aces (measured as the number of web pages mentioning them) grows exponentially with their achievement (measured as the number of their victories). One may hypothesize that a similar relationship exists between fame and achievement in other professions including those where an unquestionable and universally accepted measure of achievement does not exist. One can then compute the ratio of achievements of two people as the ratio of the logarithms of their fame.
Table 1 below shows the results obtained by Claes and de Ceuster using this method. You can see that the differences in achievement are far smaller than the differences in fame. This is, of course, similar to what happened with Nobel Prize winners in Physics2.
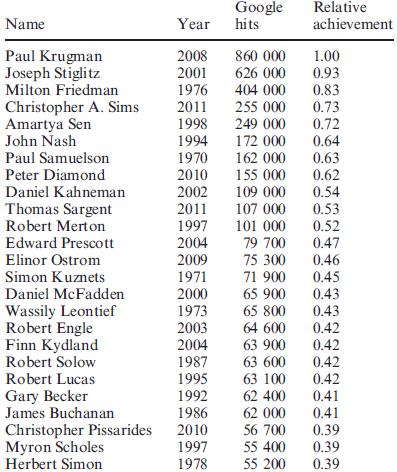
Table 1 Fame (in Google hits) and relative achievement of the 25 most famous economists alongside the years they received their Nobel Prizes. This is the top of Table 11, which contains the data for all 69 Laureates.
One way to use the data in Table 1 is this: suppose that you know the work of one of the listed economists and can judge the magnitude of their contribution. Now you immediately get a sense of the magnitude of achievement of the other economists on the list. I happen to know a little about the work of John Nash, who is number 7 on the list. He received his Nobel Prize for Nash Equilibrium in Game Theory. To illustrate this scientific concept, economics textbooks3 use the so-called Prisoner’s Dilemma:
The police arrests two criminal partners and puts each in a solitary confinement where they cannot communicate. If neither of the criminals cooperates with the police, they will send each criminal in jail for one year. If one criminal testifies against his partner, he will go free while the partner will get three years in prison. If both prisoners testify against each other, both will get two years in jail.
Nash Equilibrium is when no game participant can improve his outcome when all other participants keep their strategy. In Prisoner’s Dilemma, such equilibrium happens when both criminals testify against each other and get two years each. If either of them changes strategy, he gets an extra year in jail. Of course, both criminal partners will be better off if neither of them testify since they will get one year each. However, in such case either of them can improve his outcome by testifying. Nash Equilibrium in Prisoner’s Dilemma shows that egoistic strategies in non-cooperative games can lead to common bad.
Another example of Nash Equilibrium, this time in Tosca-Scarpia game, describes Dr Fox in his lecture.
Now you will be familiar with Nash’s contribution to science and can form a judgment of its magnitude. According to the table, the number 1 economist, Paul Krugman, achieved about 50% more than Nash. Keep in mind, however, that I did not describe Nash’s work proper. He studied games with an arbitrary number of players each of whom has an arbitrary number of strategies. He proved4 that every such game has a Nash Equilibrium point. He demonstrated the vitality of his approach using an example of a three-person poker game4. It is far more difficult to form a judgment of this mathematical work. It may be easier, however, to form a judgment of its relevance to Economics.
References
- Claes, A.G. P. and De Ceuster M. J. K. (2013) Estimating the economics Nobel Prize laureates’ achievement from their fame, Applied Economics Letters, 29, 884-888 http://dx.doi.org/10.1080/13504851.2012.758836
- Simkin, M. V. and Roychowdhury, V. P. (2011) Von Richthofen, Einstein and the AGA, Estimating Achievement from Fame, Significance, 8, 22–6. http://onlinelibrary.wiley.com/doi/10.1111/j.1740-9713.2011.00473.x/abstract
- Varian, H. (1999) Intermediate Microeconomics. W.W. Norton & Company. New York.
- Nash, J. (1951) Non-Cooperative Games. Annals of Mathematics 54, 286-295 http://www.jstor.org/stable/1969529




