
In his paper Probability, Rarity, Interest, and Surprise, Warren Weaver wrote that an event is surprising 'not because its probability is small in an absolute sense, but rather because its probability is so small as compared with the probabilities of any of the other possible alternatives.' Thus rarity is a necessary but not a sufficient condition for surprise.
Suppose that events V1, V2, … occur with probabilities p1, p2, …; the surprise index associated with an event Vi, say SIi, compares the expected value of these probabilities with pi, and this can be written as SIi = E(p)/pi = (p12 + p22 +… )/pi. Following Weaver, this quotient measures 'whether the probability realised, namely pi, is small as compared with the probability that one can expect on the average to realise, namely E(p). If this ratio is small and SI correspondingly large, then one has a right to be surprised'. Weaver went on to suggest the classification shown in Table 1:
| Table 1: Weaver's interpretation of SI values | |
| <5 | Not surprising |
| 10 | Begins to be surprising |
| 1,000 | Definitely surprising |
| 1,000,000 | Very surprising |
| 1,000,000,000,000 | Miracle! |
I analysed frequencies of goals scored against Brazil in all 20 World Cup finals from 1930 onwards. I excluded goals scored at extra times and penalty shootouts. Brazil has played 103 matches including this defeat against Germany and its follow-up, another defeat, this time 3-0 against Holland in the match to determine the third place. The distribution of goals scored against Brazil in all World Cups, taken from FIFA's website is shown in Table 2.
| Table 2: Frequencies of goals scored against Brazil in 103 World Cup finals' matches | ||||||||
| Goals | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Frequency | 44 | 35 | 15 | 6 | 2 | 0 | 0 | 1 |
Clearly seven goals is a discrepant observation, and this is confirmed by Grubbs' test for one outlier which yields p-value = 9.5×10-7, but, as we have seen, this is not necessarily the same as being surprising.
Though often goals scored against a a team follow a Poisson distribution, these data show evidence of overdispersion: sample mean = 0.951, sample variance = 1.341, and the Neyman-Scott statistic leads to reject the null hypothesis of Poissoness (p-value< 0.001). A negative binomial model fitted the data significantly better than a Poisson model, and its probabilities can be seen in Figure 1.
Figure 1: Empirical probabilities and probabilities from the negative binomial model
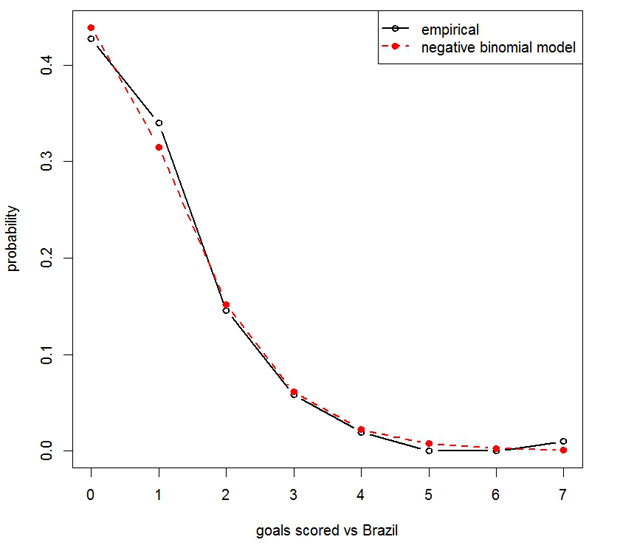
Using this model, I calculated the surprise index for values of goals scored against Brazil between 0 and 8 (Table 3).
| Table 3: Surprise index values from the negative binomial model | |||||||||
| Goals | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Surprise Index | 0.7 | 1.0 | 2.1 | 5.2 | 14.3 | 24.0 | 129.3 | 412.0 | 1348.5 |
This brief analysis implies that last week's result is rare and very much out of line with Brazil's previous performances in World Cup finals, but can't be considered definitely surprising according to Weaver's criterion – to establish such result at least another goal would have been needed.
Randomness is an integral part of football at all levels, and sometimes these uncontrolled variations produce strange, seemingly extreme results but we shouldn't be completely surprised when they appear, these things happen: as RA Fisher wrote: 'For the "one chance in a million" will undoubtedly occur, with no less and no more than its appropriate frequency, however surprised we may be that it should occur to us.'
Anyway, it’s only a game…




