
Unlike the Super Bowl – the NFL's championship game – North America's other major sports all use seven-game playoff series to decide that year's winner. In each playoff, two finalists share hosting duties, with one given home field (or rink, or court) advantage, playing four home games to their opponent's three. This means you get some variation in how fixtures are arranged: in the National Basketball Assocation (NBA) and NHL, this lucky team hosts games 1, 2, 5, and 7, while in baseball they get to play their first two and last two games at home.
Of course, not every series will go to the seventh game, and so sometimes the 'home advantage' won't materialize at all, but the order in which games are played does have another important impact. The Penguins won the Stanley Cup at the Sharks' SAP Center (somewhat predictably nicknamed 'the Shark Tank'), and so the on-ice celebrations were met with an appropriately frosty reception from the crowd. The Warriors, meanwhile, have the chance to match this feat in front of the Cavs' fans later this week. There's little question that a team winning in front of their own fans makes for a more dramatic (and less awkward) conclusion to a season, so can we change the playoff structure to make this a little more likely?
If we take our seven-game series and assume one team – who, for convenience, I'll call the higher seed – will host four games, and the other three, there are 35 possible ways to arrange the fixtures. For example, the higher seed could host the first four games before playing the final three on the road, or you could switch it around and have their three away games first before coming back home for the rest of the series, with a whole range of alternatives in between.
There are, however, quite a few bits of conventional wisdom that may make certain arrangements of fixtures unsuitable, such as teams getting 'on a roll' from a run of home games, or consecutive games in one city leading to fewer rest days, potentially giving an advantage to younger teams. The legitimacy of these theories is somewhat questionable, and so I'm largely going to ignore them in addressing this question. One thing I will factor in, though, is that both teams should get to host at least two games (a rule highly unlikely to be broken in the real world, as ticket revenues in the playoffs are a huge financial boost). This translates to the first four games of the series being evenly split between the two host cities, as is seen in all three of the major US leagues, and reduces our possible formats to a more manageable 18.
The other assumption I'm going to make is that all games are independent events, so the probability of a team winning game 7 (should the series get that far) is the same as them winning game 1, regardless of what has happened in between. This will doubtless seem an unreasonable assumption to many, but I couldn't find any sources that strongly contradicted it in the case of playoff series – and it does make our task easier.
Our goal is to calculate the probability that a particular arrangement of fixtures results in the championship being won by a team playing at home. To do so, we first have to list all the sequences of results that end up with a team winning their fourth game in front of their own fans, work out the probability that particular sequence of results will happen, then add up these probabilities for all of those sequences.
For example, if we take the series between the Penguins and the Sharks, we would have seen a home team win if the Sharks had won the series 4-0 or 4-2 (since they hosted games 4 and 6), or if the Penguins had won the series 4-1 or 4-3 (since they hosted games 5 and 7). We then just need to add up the probability of each of those scorelines actually happening to get the overall chance of a home win. For some it's easy: the Sharks winning 4-0 means they take four games in a row, so if the probability of a Sharks win in one game is, say, 50%, the probability they win four games in a row is just 0.5 x 0.5 x 0.5 x 0.5, or 1 in 16. (This is where assuming games are independent events comes in handy, as we can just multiply the probability of each event together.) For the other scorelines we have to be more careful. A 4-2 Sharks win, for instance, could come from a sequence of 3 wins, 2 losses, then a win, or a sequence of 2 losses followed by 4 straight wins, along with a bunch of other combinations. For each of these we can still just work out the probability of the result of each game and multiply them together, but we have to make sure we cover all the possibilities.
From here, all we need now are those game-by-game probabilities; in other words, what were the chances of the Sharks winning any given game? We could suppose every game is like a coin toss, with both teams standing a 50% chance of winning, but that's pretty boring (and unrealistic). Instead, we may suppose that the team playing at home has a higher chance of winning – there's a reason it's called a home field advantage, after all. A bit of googling (see here and here) suggests that baseball and hockey teams average a 55% chance of winning at home, while for basketball teams it creeps up to 60%. Regardless of whether we choose 55%, 60%, or any other number (bigger than 50%), six new playoff formats lead to a better overall chance of a home team win than the current formats used by the NHL, NBA and MLB. You can see these in the table below, where I've taken inspiration from the Stanley Cup playoffs and let the Penguins host four games and the Sharks three.
Table 1. Arrangement of playoff fixtures giving the highest chance of the championship being won at home. (Host team indicated by their respective animal.)
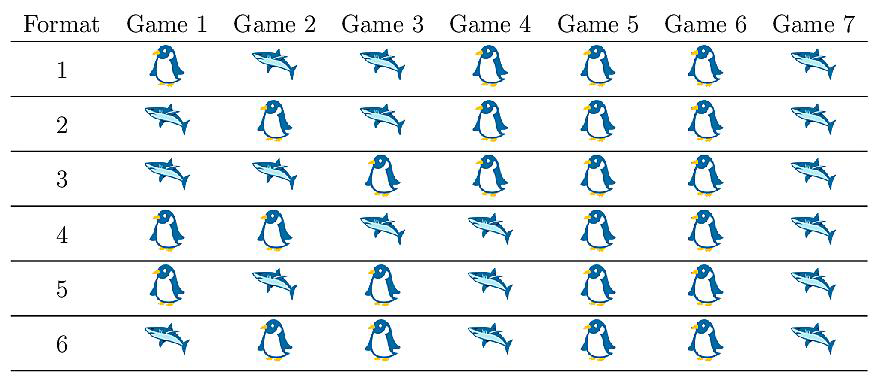
Now admittedly, these formats aren't much better than what currently happens. If we say the team playing at home has a 60% chance of winning any particular game, for instance, then the current playoff structures lead to a team winning the championship at home 58.2% of the time. For one of these six alternatives the probability is only slightly higher at 59.5%. They do demonstrate an interesting pattern though – only the ordering of the last three games matters. In this case, as long as games 5 and 6 are hosted by the Penguins, and game 7 by the Sharks, then it doesn't matter how you arrange the first four fixtures. The precise reasons are a little hidden in the underlying algebra, so I'll leave that to the interested reader.
Moving on, let's suppose that our assumption that either team has the same chance of winning at home isn't quite accurate enough. Instead, what if the higher-seeded team is, in fact, better? We can simulate this by adjusting our probabilities slightly. Previously we'd decided that if the Penguins have a 60% chance of winning at home, then they have a 40% chance of winning away. But what if we thought the Penguins (who performed slightly better in the regular season) actually had a 50% chance of winning in the Shark Tank; would that make any difference to our proposed playoff structures? The answer, it turns out, is a resounding 'yes'. In that scenario the odds of the championship being won by the team at home drops to 52.4% under Major League Baseball's current playoff format, and 53.7% for the NHL and NBA formats. In contrast, if we choose one of the first three playoff structures in Table 1 (i.e., where the Penguins host game 4), the odds of a championship win in front of a home crowd jump to a whopping 62.4%. If we picked the bottom three structures (perhaps to avoid a team hosting three games in a row) we still get odds of 57.4% – an improvement of 4-5 percentage points – and the difference between the current playoff formats and our 'optimal' ones only increases as our faith in the higher-seeded team grows. In fact, as soon as we suppose the higher seeded team is genuinely better, the MLB format is one of the three joint-worst ways to arrange the fixtures; although given how that team is chosen this may not be too much of a concern.
We may not be happy with the lower seeded team having to host game 7, however, so as a final note I present the best formats where this doesn't happen in Table 2 (below). These still comfortably outperform the MLB/NHL/NBA formats (by 4-6 percentage points; the top three rows are fractionally better than the bottom three) without the slightly awkward feeling that the lower seeded team is getting short-changed by hosting the final game.
Table 2. Arrangement of playoff fixtures giving the highest chance of the championship being won at home, assuming higher seeded team hosts the final game, and has a better chance of winning overall. (Host team indicated by their respective animal.)
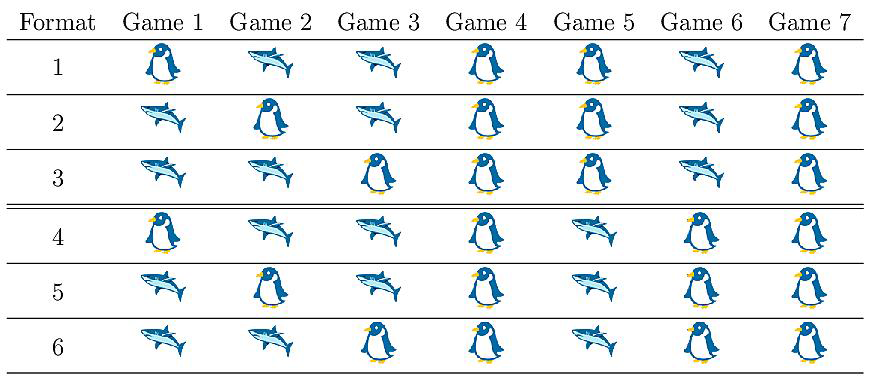
So there you have it: if you want to avoid an awkward awards ceremony in front of disappointed fans you can do a fair bit better than what's currently on offer. While there are various practical considerations I've overlooked, it wouldn't require too much of a change to switch to one of the above formats. You can argue about momentum, or the value of getting off to a good start in a series, but for me nothing beats a home-town triumph. (Unless, of course, we're talking about Euro 2016.)
- Michael Wallace is a post-doctoral fellow in the department of epidemiology, biostatistics and population health at McGill University, Canada. He is also a member of the Significance editorial board.




